[반도체 소자] 반도체 기초-1
1. 반도체
: 도체와 부도체 사이 비저항을 가지는 물질 또는 그러한 물질을 이용해 외부 전기신호를 전달, 증폭하는 소자
1) 발전방향
- 무어의 법칙: 반도체 집적도가 1년 6개월마다 2배씩 증가한다는 법칙
인텔의 고든 무어가 1965년에 주장한 후 반도체 기술은 무어의 법칙을 따라 발전해왔다.

- 반도체 미세화(Shrink)
: 하나의 웨이퍼 당 생성되는 Die 수 증가로 가격 감소
트랜지스터의 채널이 짧아질수록 전자이동거리가 감소해 소비전력 감소, 발열 감소, 성능 증가
- Node: 원래 채널 선폭(게이트 길이)의 절반을 의미
, 그러나 최근에는 공정스케일과 노드 명칭이 일치하지 않고 있으며 회사마다 명칭이 다르다.
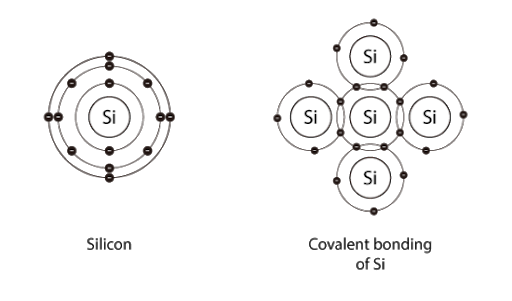
2) Si
- 원자번호 14
- 최외각 전자 4개, 주위 4개 원자와 결합
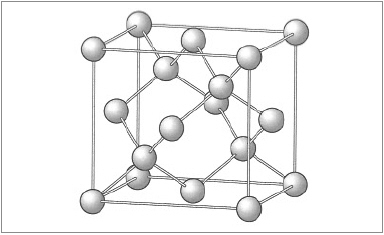
- 다이아몬드 입방체, 격자 상수= 5.43Å
3) 에너지 밴드갭
: 원자내 불연속적 에너지 준위 존재
원자들간 거리 가까워지며 파울리 배타원리에 따라 에너지 밴드가 형성됨
*파울리 배타원리- 주양자수, 부양자수, 자기 양자수, 스핀 양자수가 모두 동일할 수 없다.

- 실리콘의 에너지 밴드

- 가전자대 (Valance band): 속박된 전자가 존재하는 에너지 대
Ev는 가전자대의 최대에너지
- 전도대 (Conduction band): 전자가 자유롭게 움질일 수 있는 에너지 대
Ec는 전도대의 최소에너지
- 금지대(Forbidden band): 가전자대와 전도대 사이 전자가 존재할 수 없는 에너지 대
- 에너지 밴드 갭(Eg): 가전자대와 전도대의 에너지 차이
에너지 밴드갭에 따라 절연체(5eV이상), 반도체, 도체(금속)로 구분된다.

4) 에너지 상태 밀도(DOS,Density Of State)
: 캐리어가 점유할 수 있는 에너지 준위 밀도 [개/cm3.eV]
가전자대, 전도대의 밀도는 낮음

- 페르미 디락 분포 함수(Fermi-Dirac distribution)
: 에너지준위에서 전자 존재 확률 분포 함수
=1/ 1+ exp(E-Ef/kT) *k(볼츠만 상수)=8.62x10^-5 eV/K , 1eV = 1.6 × 10^-19J

- 페르미 레벨 (Fermi level,Ef): 절대영도(0k)에서 전자의 최대 에너지 준위
열 평형에서 소자 내 페르미 준위는 모든 영역에서 일정
절대영도에서 페르미 레벨까지 전자 존재확률= 1, 페르미레벨 이상에서 전자 존재확률= 0
0K 이상에서 페르미 레벨의 전자 존재확률= 50%
온도가 높아 질수록 페르미 레벨 이상에서 전자 존재 확률 상승
Ei= 진성 반도체에서의 페르미 레벨
- 일함수(Work function): 페르미 레벨과 진공 에너지 준위(Vaccum level)의 에너지 차이
- 전자친화도(Electron affinity): 중성 원자 1mol이 전자 1mol을 얻어 에너지준위가 낮아지면서 방출하는 에너지 [KJ/mol]
전도대와 진공 에너지 준위의 에너지 차이
중성 원자 하나가 전자하나를 얼마나 쉽게 받아들일수 있는지에 대한 척도